ピラミッドの建造と位置の設定

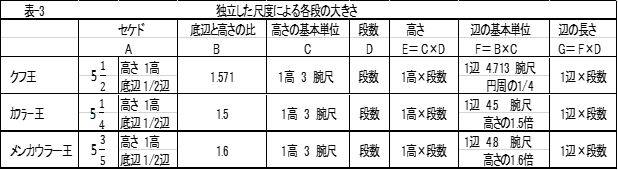
独立した尺度による設計について。　　　　　　　　　　　　　　　　　　　　　　　　　　　ピラミッドの頂点から最下部までの大きさを腕尺で表すと、クフ王のピラミッドでは高さが300腕尺、底辺が471.3腕尺、カフラー王のピラミッドでは高さが300腕尺、底辺が450腕尺，メンカフラー王のピラミッドでは高さが150腕尺、底辺が240腕尺となる。高さの基本単位を腕尺3単位にすると、底辺の基本単位はクフ王のピラミッドでは4.713腕尺、カフラー王のピラミッドでは4.5腕尺、メンカウラー王のピラミッドでは4.8腕尺となる。もし、これらの数値を使った場合、数値が大きいため、計算、設計、高さと長さの測定、位置の設定、角度の設定、石の加工などが複雑になる。この問題を解決するには、高さと底辺の長さの数値を端数の無い、小さい整数にする必要がある。そのために、基本単位を独立させたと考えられる。高さの基本単位を 「1高」、辺の基本単位を 「1辺」 に設定すると、各段の高さは 「1高×段数」、底辺の長さは 「1辺×段数」 となり、整数で表されるため、扱いやすい数値となる。また、基本単位を使って角度を決める場合、高さの1高に対して底辺の長さが1/2辺の直角三角形の角度となる。その理由をセケドの計算から確かめると、セケドの計算式は（底辺×1/2×7（バーム）÷高さ）となるので（図-1）、クフ王のピラミッドでは、高さの1高が3腕尺、底辺の長さの1辺が4.713腕尺のため、（4.713×1/2×7÷3＝

5.4985＝5.5）となり、セケド5・1/2となる。カフラー王のピラミッドでは、高さの1高が3腕尺、底辺の長さの1辺が4.5腕尺のため、（4.5×1/2×7÷3＝5.25＝5+1/4）となり、セケド5・1/4となる。メンカウラー王のピラミッドでは、高さの1高が3腕尺、底辺の長さの1辺が4.8腕尺のため、（4.8×1/2×7÷3＝5.6＝5+3/5）となり、セケド5・3/5となる表-3）。

建築方法について　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　基本単位を基にしたピラミッドの模型は、底辺の長さが1辺の正四角形で、高さが1高の四角錐となる。従って、壁面の角度は、高さが1高、底辺が1/2辺の直角三角形の角度となり、稜線の角度は、底辺が1/2辺の正四角形の対角線と高さが1高の直角三角形の角度となる。この角度の設定方法は簡単であり合理的である。ピラミッドの建造には基本単位を基にした定規を使用したと考えられる。クフ王の定規の作成は、半径が腕尺3単位の円の円周にヒモを這わせて、次に、そのヒモを4等分して長さの基本単位の1辺とした。カフラー王とメンカウラー王の定規は、腕尺の定規で（1+5/10）と（1+6/10）の長さを計り、その長さの3倍を1辺の長さとした。　対角線の定規の作製は、基線ａの上に1/2辺の間隔をあけて、半径が1/2辺の円を描く。この2つの円の交点を繋ぐと、その線ｂは基線ａに直角に交叉する。この線を使って、辺が1/2辺の長さの直角三角形を描くと、斜線の長さが対角線の長さとなる（図-7）。この定規を使って、四角の石を作ると、高さが1高、上面の1辺が1/2 辺、下面の1辺が1辺の台形となる。また、高さと辺の長さの定規を同じ比率で短くすると、同じ角度で大きさの異なる石を作製できる

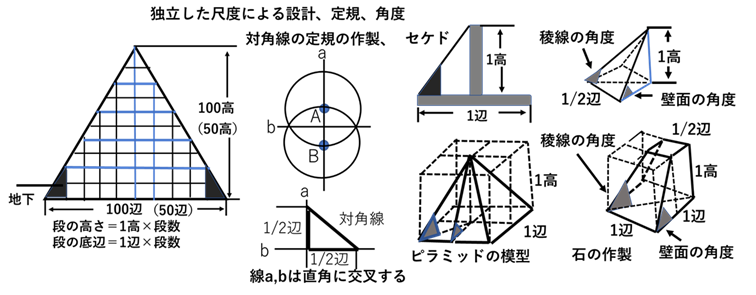
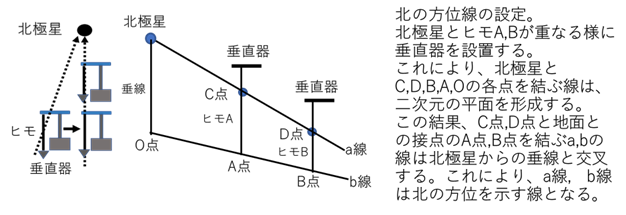
（図-7）。ピラミッドの建造は、最初に位置を設定するため、北の方位を決める必要がある。それには水平な平面に、北極星に向けて2基の垂直器を設置して、錘の付いたヒモを吊り下げる。次に、北極星と垂直器の2本のヒモが一直線になる様に位置を調整する。この２個の錘と平面との接点を繋ぐ線が、北の方位線となる（図-8）。なお、地球から北極星までの距離は無限大のため、北極星から観る地球は点となる。そのため地球上の方位線は同一線となり、地球上の北の方位線は平行になる。

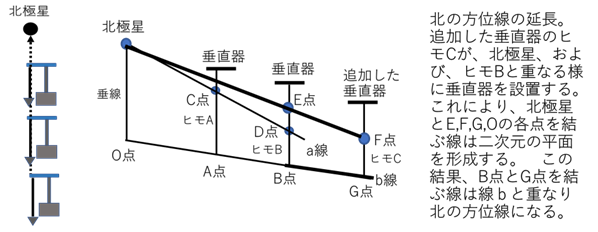
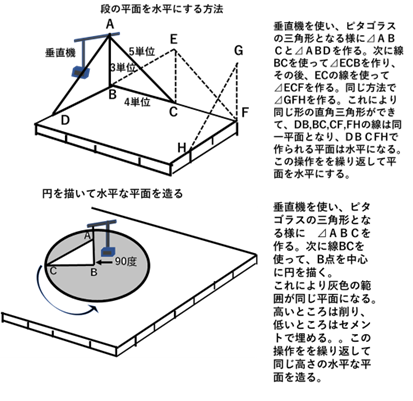
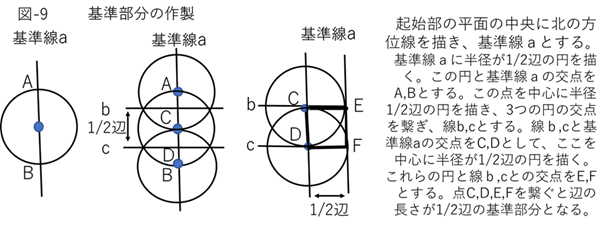
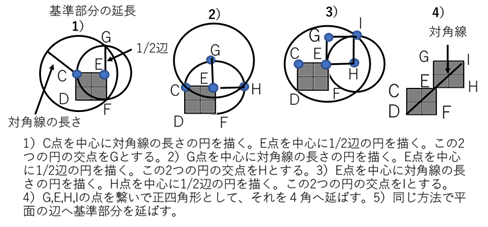
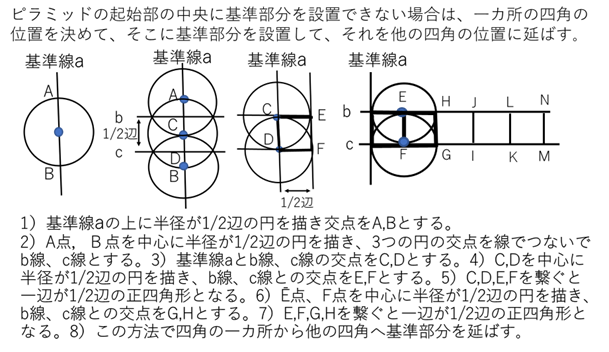
この線を基に、ピラミッドの四角の位置、辺と対角線の方向を設定する。ピラミッドの位置の設定は、最初に、ピラミッドの起始部の平面を水平にして、その中央に北の方位線を描き、この線を基準線ａとする。基準線ａに半径が1/2辺の円を描く。この円と基準線ａの交点をA.Bとしてここを中心に、半径が1/2辺の円を描き、3つの円の交点を繋いで、その線をb,cとする。線ｂ,cと基準線aの交点をＣ,Dとして、ここを中心に半径が1/2辺の円を描く。これらの円と線ｂ,cとの交点をＥ,Ｆとする。これらの点Ｃ,D,Ｅ,Ｆを繋ぐと、辺の長さが1/2辺の正四角形となりこの部分を基準部分とする。この四角形の対角線がピラミッドの対角線となる（図-9）。次に、基準部分を辺縁と四角に向かって延長する。しかし、その方向を正確に設定するため、基準部分の４角の位置を正確に設定する必要がある。そのために、1）C点を中心に対角線の長さの円を描く。次に、E点を中心に1/2辺の円を描く。この2つの円の交点をGとする。2）G点を中心に対角線の長さの円を描く。その後、E点を中心に1/2辺の円を描く。この2つの円の交点をHとする。3）E点を中心に対角線の長さの円を描く。H点を中心に1/2辺の円を描く。この2つの円の交点をIとする。4）G,E,H,Iの点を繋いで正四角形として、それを４角へ延ばす。5）同じ方法で平面の辺へ基準部分を延ばす。この方法により基準部分の正確な位置を設定して、四角の位置を設定する図-10,11）。

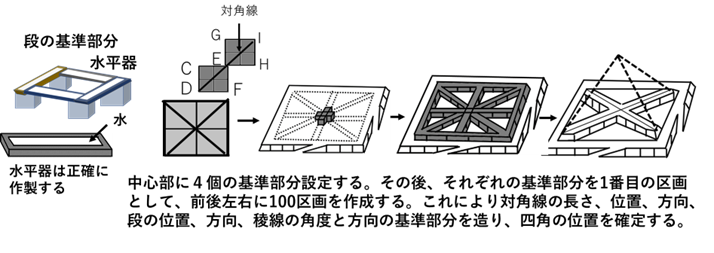
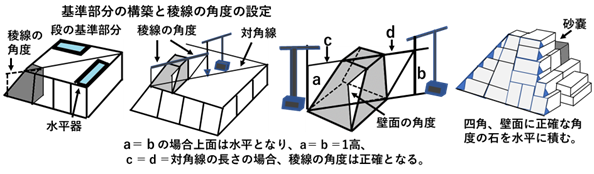
基準部分と段の水平状態の設定は、水を満たした丸木舟の様な構造の、長方形の木製の水平器を置いて、その水面より求める。垂直の位置は、垂直器から錘の付いたヒモを吊り下げて設定する。稜線の角度は、四角の石の上面と基準部分の対角線を基に、石の外部に形成される直角三角形の高さと底辺の長さを測って調べる。角度が異なる場合は、正確な角度の石に取り換える、あるいは、修正する。四角と壁面には、正確な角度の石を水平に積む。これにより、石の大きさに関わらず、稜線と壁面は一点に収束する。また、内部には四角形の石を積み、さらに、石の破片は、その処理と石の節約、および、重力の緩衝作用の目的で、砂嚢に詰めて適切に配置する。この様な方法で四角錐のピラミッドを建造したと考えられる（図-12）。

7）土台部分の状態によるピラミッドの高さと底辺の長さの修正方法について　　　　　　　　高さは頂点より最下部までの段数で決められるが、ピラミッドが岩盤の上に建造されている場合、地下部分の建造が行われないため、高さと底辺の長さの決定方法について検討した。　　　クフ王のピラミッドは高さが280腕尺、底辺の長さが440腕尺に設定されている（表-2）。しかし、その理由が明らかでない。ピラミッドの角度はセケドに基づいて設定されている。その基準は、クフ王のピラミッドのセケドを、作図により計算する方法から求められている。それは直角三角形の高さを7段（7腕尺）とした場合の底辺の長さから計算される（図-3）。そのため、高さの腕尺7単位を基準値にして、その倍数を計算した。頂点から最下部までは100段×3腕尺=300腕尺のため、300腕尺÷7腕尺＝42.86倍となる。この中の40倍の部分を設計、測量、建造の行い易い高さとして、7腕尺×40＝280腕尺を地上部分に設定したと考えられる。また、セケドを表す二等辺三角形の底辺の長さは11腕尺となるので（図-3）、その40倍の440腕尺を底辺の長さにしたと推測した。しかし、段数を基に高さと底辺の長さを検討すると、段数は1段が3腕尺のため、280÷3=（93+1/3）＝93.33段となり端数の付いた数値となる。その解決策として、地面より2/3段低い94段目を地上部分の建造の起点として、完成後に掘り下げた所を埋めて、地上の起始部を（93+1/3＝93.33）段に戻したと考えられる。また、底辺の長さは94段目より「1辺×段数」で設定されるため、93.33段の底辺は93.33辺となり、腕尺で表すと1辺が4.713腕尺のため93.33×4.713＝439.86＝440腕尺となる。　　　　　　　　　　　　　　　大きなピラミッドの建築方法はクフ王のピラミッドで完成されたと考えられる。クフ王とカフラー王のピラミッドの頂点から最下部までの高さは300腕尺で同じであるが、地上部分の高さはクフ王のピラミッドは280腕尺、カフラー王のピラミッドは274.5腕尺（表-2）で、5.5腕尺の差がある。　しかし、その数値は小さいため有意な差ではないと考えられる。このことを考察すると、初めは、カフラー王のピラミッドは、クフ王のピラミッドの高さと同じに設計されたと推測される。しかし、カフラー王のピラミッドの建築地盤がクフ王の地盤より高いため、クフ王のピラミッドの高さに合わせるために、高さを274.5腕尺に修正したと考えられる。これに基づいて段数を計算すると、段数は274.5÷3＝91.5＝（91+1/2）段となり、建造し易い数値となる。しかし、ピラミッドと地面の接続部分を整地するために深さが必要となるため、1/2段下の92段目をピラミッド建造の起始部として、完成後に掘り下げた1/2段の部分を埋めて、（91+1/2）段の高さに戻したと考えられる。底辺の長さは1辺が4.5腕尺のため、91.5段目は91.5×4.5＝411.75腕尺となり（表-2）の結果の411.84腕尺と同じになる。メンカウラー王のピラミッドの高さは125.01腕尺（表-2）である。頂点から最下部までの高さは150腕尺のため、地下部分の高さを25腕尺にして、地上部分と地下部分の高さの比率を5対1に設定したと考えられる。地上部分の高さの125.01腕尺を125.1腕尺に修正すると、段数は125.1÷3＝41.7＝（41+7/10）段となる。そのため、地面より3/10段低い42段目を地上部分の起始部としてピラミッドを建造して、完成後に掘り下げた3/10段の部分を埋めて、地上部分の高さを41.7＝（41+3/10）段に戻したと考えられる。底辺の長さは1辺が4.8腕尺のため、41.7段目は41.7×4.8＝200.16腕尺となり（表-2）の結果の200.016腕尺とほぼ同じ長さになる（図-14）。