作図で円周の長さ求める方法

古代の円周の長さの求め方

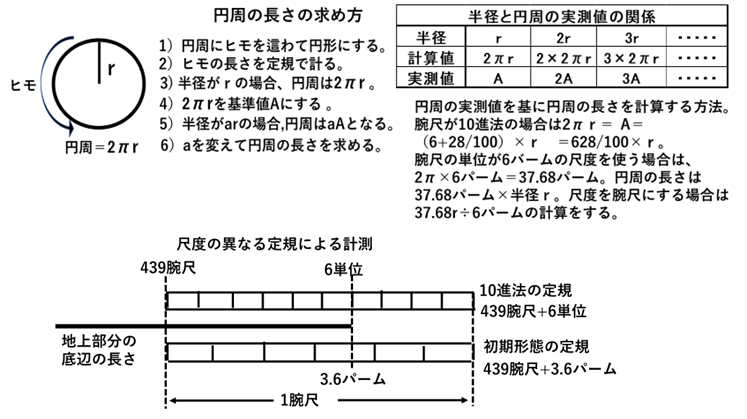
古代のエジプトでは、円周の長さを2πrの計算で求めることは出来ない。そのため、別の方法で求めたと考えられる。それは、円を描き、その円周にヒモを這わせて、そのヒモの長さを定規で計る。その数値が、円周の長さになる。この方法を使って、半径の異なる幾つかの円周の長さを計り、それを比較する。例えば、半径の基本単位をｒにすると、円周の長さは2πrになる。これを基準値のAに設定する。次に、ｒをa倍にすると、2πaｒはaAになる。その結果、aを1、2、3、・・・に変えると、半径は1r、2ｒ、3ｒ、・・・になり、円周の長さは1Ａ．2Ａ、3Ａ、・・・になる。これにより、半径と円周の長さが比例することが解る。　この方法で、一度、半径の基本単位を決めると、それに対する円周の長さが決まるため、その後、円周の実測を行わずに、簡単な計算で円周の長さを求めることができる。例えば、半径を腕尺1単位にすると，円周の長さの計算値は2π×1腕尺＝2×3.14×1＝6.28腕尺になる。この長さを腕尺の定規で計ると、π＝3.14は不変の定数であるため、尺度の単位を10進法にすると尺度の違いに関わらず、実測値は（6+2/10+8/100）の目盛りで示される。そのため、半径がｒ腕尺の場合の円周の長さの実測値Aは（6+2/10+8/100）腕尺×ｒ＝628 /100×ｒ腕尺になる。なお、1/10腕尺の目盛りは1腕尺を10単位に分割し、さらに、1/100腕尺の目盛りは1/10腕尺の目盛りを10単位に分割して使用したと考えられる。

また、円を描くのに初期形態のロイヤルキューピットの単位が6バームの定規を使用した場合は、腕尺1単位を6バームにして、円周の長さの計算をする。円周の長さは2π×6バーム＝37.68バームになり、円周の長さの実測値として定規で示される。半径ｒの円周の長さは（37.68バーム×ｒ）になるが、この数値を腕尺に変換するには（37.68バーム×r）÷6の計算をする。さらに、この数値を腕尺とバームの数値で表すには、腕尺1単位が6バームであるため、37.68×ｒを6バームで割って、さらに、小数点以下の数値に6バームを掛けてバームの数値で表す。腕尺1単位の円周の長さは37.68÷6＝6.28腕尺になるが、小数点以下は0.28×6バーム＝1.68バームになる。この結果、37.68バームは（6腕尺+1.68バーム）の目盛りで示される。従って、腕尺1単位が6バームの初期形態の尺度で円を描いた場合、円周の長さの計算は（6腕尺+1.68バーム）×半径ｒになる。

これらの計算方法は、作図による正確な円周の長さの求め方として、有効な方法と考えられる（図-5）。この方法でクフ王のピラミッドの底辺の長さの計算を10進法の腕尺で行うと、頂点から最下部までの高さは100段　（300腕尺）であるので、底辺の長さの総和は628/100×300＝1884腕尺になり、一辺の長さは1884×1/4＝471腕尺になる。地上部分の高さは93.2段（280腕尺）のため、底辺の長さは628/100×280×1/4＝439.6腕尺になる（図-2）。　また、初期形態の腕尺の単位が6バームの尺度を使って計算をすると、円周の長さは37.68バーム×半径ｒになるので、クフ王のピラミッドの最下部の底辺の長さは37.68バーム×300腕尺×1/4＝2826バーム　になる。これを腕尺の単位に変換すると2826÷6＝471腕尺になる。　地上部分の底辺の長さの計算は（37.68バーム×280腕尺×1/4÷6バーム＝439.6腕尺になる。この数値を腕尺とバームの単位で表すため、小数点以下の0.6腕尺に6バームを掛けると0.6×6＝3.6バームになる。この結果、439.6腕尺は439腕尺+3.6バームになる。また、この計算を半径が腕尺1単位の円周の長さが（6腕尺+1.68バーム）の単位を使って行うと、（6腕尺+1.68バーム）×280腕尺＝（1680腕尺+470.4バーム）になる。470.4バームを腕尺とバームに分けると468/6腕尺+2.4バームになる。そのため（1680腕尺+470.4バーム）＝（1758腕尺+2.4バーム）になる。この数値は底辺の長さの総和のため1辺の長さは（1758腕尺+2.4バーム）×1/4＝（439.5腕尺+0.6バーム）になる。この中の0.5腕尺をバームに変換すると（0.5腕尺×6バーム＝3バーム）になる。その結果、（439.5腕尺+0.6バーム）＝（439腕尺+3.6バーム）になる（図-5）。

Follow me!