ピラミッドの仮設部分に第1運搬路を設計

1）運搬路の設計について

ピラミッド建造の中で、資材を運ぶ運搬路は、建築を行うための基本構造である。どのような状況下でも運搬を可能にする運搬路が、ピラミッド建設の絶対条件である。　また、限られた期間内に建造するには、一定の時間に運ぶ石の量を多くする必要がある。そのために運搬経路をピラミッドの四面に設置したと考えられる。しかし、その構築に要する　石の量を最小にするために、ピラミッドの1面に突出部分を造り、それに設置する運搬路と、ピラミッドの3面に直接設置する運搬路の2種類を建造したと推測した。また、突出部分の体積を小さくするために運搬路の基本形を3種類作製して使用したと考えられる。運搬路を幾何学的に設計するためには、高さと底辺の長さを表す単位とその数値を、整数で表す必要がある。そのため、高さと底辺の長さの尺度を独立させて使用した。これにより1段の高さの差は1高となる。１段の底辺の長さの差は1辺となり、片側の差は0.5辺となる。この数値は運搬路を設計する際の基本となる。

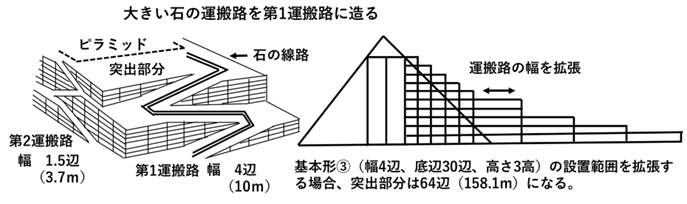
2）　突出部分に併設する第1の運搬路について　　　　　　　　　　　　　　　　　　　　　この運搬路は、外側に突出部分を造り、そこに運搬路を階段状に設計するため、幅と勾配を自由に設計できる。幅を広くするには、高さの単位をピラミッドの高さの単位と同じにして、幅を広げた基本形を作る。例えば、大きい石の運搬路を第1運搬路に造る場合は基本形の幅を4辺（10ｍ）にして、基本形①を（幅4辺、底辺10辺、高さ1高）、基本形②を（幅4辺、底辺20辺、高さ2高）、運基本形③を（幅4辺、底辺30辺、高さ3高）にして、必要とする高さまで設置する。もし、13段目より93段目（地面）まで幅の広い基本形を設置した場合、基本形の設置数は基本形①が11基、基本形②が5基、　基本形③が20基で合計36基になる（図-20，21）。基本形の幅を1.5辺から4辺に広げると基本形1基の増加分の長さは（4-1.5=2.5辺）となり、36基では2.5×36＝90辺になる。そのため、突出部分の長さは、幅が1.5辺の場合の突出部分の長さの14辺に増加部分の90辺を加えて（14辺+90辺＝104辺）になる。メートル法で表すと、1辺が2.47ｍのため2.47×104辺＝258.88ｍになる（図—22参照）。また、幅の広い基本形の設置部位を，基本形➂の設置範囲に限定すると、突出部分の増加分は2.5辺×20基＝50辺となる。それにより突出部分は14+50＝64辺となり　メートル法で表すと2.47×64＝158ｍになる。これにより、大きい石の運搬は必要な時に何時でも出来る状態になるが、突出部分に要する石の量は増加する。

勾配を低くするには、高さを一定にして底辺を長くした運搬路を造る。幅と底辺の長さを変える方法を組み合わせると、幅が広く勾配の低い運搬路を設計できる（図-25）。例えば、底辺の長さを1.5倍にすると、基本形①の底辺は15辺となり、基本形➁は30辺、基本形③は45辺となる。基本形①の底辺は15辺のため、最終設置部位は15辺∔踊り場3辺=18辺の18段目となり、この基本形の角度は2.4度となる。底辺の長さを2倍にすると、基本形①の底辺は20辺、基本形②は40辺、基本形③は60辺となる。この基本形の最終設置部位は、基本形①の20辺∔踊り場3辺=23辺となり、23段目となる。この基本形の勾配は1.8度となる。以上の結果、勾配を低く設計すると基本形の底辺が長くなり、各基本形の設置できる最終到達部位は低くなり、それにより、突出部分の体積は大きくなる。また、底辺の長さに比べて角度が小さいため、石の加工は難しくなる。

Follow me!