クフ王のピラミッドのセケドの数値を5.5に設定した方法

セケドの計算の基準

　クフ王のピラミッドのセケド、および、ロイヤルキューピットの単位が7バームに設定された理由について

勾配を決めるセケドは、底辺の長さの 1ロイヤルキューピットを7バームに設定して計算をする。しかし、この7の数値が何時どのようにして決定されたのかは 明らかでない（文献-2、ｐ-154,155）。また、ロイヤルキューピットの単位について【 J・A・R レゴンは古代エジプトの尺度に関して多くの論文を出しており、その中で7バームから構成される物差しは宗教上の象徴的な要求により、新たに作り出されたという見方を示し、マスタバから発見されたチェトバと呼ばれる１ロイヤル.キュービットの六分の一の単位長を持つ寸法線の存在を根拠に挙げている。古代の尺度に関しては謎が多いが、1ロイヤルキュービットの初期形態は、6バームから構成されていた可能性を述べている 】 と発表されている（文献-2、ｐ-154）。

ロイヤルキューピットの単位について、クフ王のピラミッドのセケドの算出方法を基に検討した。クフ王のピラミッドの底辺の長さは、円周の長さから求められるため、整数ではない。その理由により、計算ができないため、作図でセケドが求められたと考えられる。

角度を表す場合、高さと底辺の長さを同じ尺度の数値で表して作図をする方法が必要である。その方法を行うため、クフ王のピラミッドでは、高さの基本単位の1高を腕尺3単位に、また、底辺の長さの基本単位の1辺を、「 腕尺3単位を半径とした円周の長さの1/4 」に設定して、二等辺三角形を描く。次に、高さを腕尺1単位の間隔に分割する。その後、辺の長さを、頂点より下方に向かって、順番に10進法の腕尺の定規で計り、辺の長さが腕尺の整数倍の段を捜す。クフ王のピラミッドでは、辺の長さが腕尺の整数倍となる最小の段は、7段目となる。その理由は、7段目の辺の長さを腕尺で表すと、底辺と高さの比が1.57のため、辺の長さは1.57×7＝10.99腕尺になる。この長さを腕尺の定規で計るとその目盛りは（10+99/100）腕尺になる。そのため、この数値の99/100腕尺を切り上げて1腕尺にして（10+99/100）腕尺を11単位にする。これにより、1段目の底辺の長さは11/7腕尺になる。この数値を11にするために腕尺を7バームに設定すると11バームになる。これは二等辺三角形の底辺の数値のため、直角三角形にすると、底辺は11÷2＝5.5 となる。これにより、セケドは5.5バームになる。　

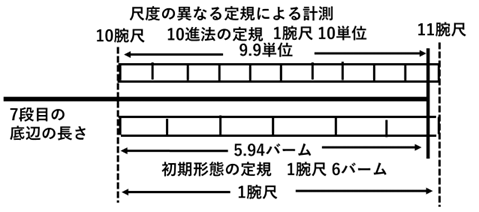
この計算方法を、初期形態の腕尺が6バームの単位を使って行うと、10進法の単位の計算と同じく、腕尺の長さの整数倍の段は7段目となり、その長さは1.57×7＝10.99腕尺になる。この数値の0.99腕尺を6バームに変換すると0.99×6=5.94バームになる。腕尺の単位が6バームのため5.94バームを1腕尺に切り上げると10.99は11腕尺になる。この数値は7段目の長さのため1段目の長さは11/7腕尺になる。この数値を11にするために腕尺の単位を7バームに変更して11バームにしたと考えられる。これは二等辺三角形の底辺の長さのため、直角三角形の底辺は11/2＝5.5バームになる（図-3）.

以上のことより、腕尺が10、あるいは、6単位であっても計測や計算をする場合、基準値を腕尺に限定して行うと10.99腕尺になるため、腕尺の単位に関わらず、得られる数値は同じになる。そのため、二等辺三角形の角度を決めるために適した数値として、腕尺の単位を6バームから7バームに変更したと考えられる。

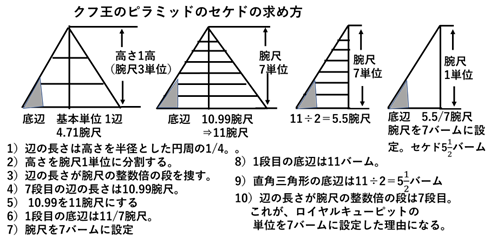
次に、別の方法でセケドを求めると、「底辺の長さは高さを半径とした円周の長さの1/4」であるので、半径が腕尺1単位の円を描いて、それにヒモを這わせて、その長さの1/4から1段目の底辺の長さ求める。計算による長さは「2π×1腕尺×1/4＝1.57腕尺」になるが、腕尺が10進法の定規で計るとこの長さの目盛りは「1+5/10+7/100」腕尺になる（図-5）。これは1段の高さを1腕尺とした場合の1段目の底辺の長さであり、二等辺三角形の底辺の基本単位である。これを基に底辺の長さが腕尺の整数倍になる段を捜す。そのため、段数をa段にして「1+5/10+7/100」腕尺」×a段の計算をする。aを1，2，3，・・・・と変えて計算をすると、aが7の場合「1+5/10+7/100」腕尺」×7＝157/100×7=1099/100＝（10+99/100）腕尺になる。この数値の99/100腕尺を1腕尺に切り上げて（10+99/100）腕尺の長さを11腕尺にする。これは7段目の底辺の長さのため、1段目の長さは11/7腕尺になる。この数値を11にするため、腕尺の単位を7バームに設定して11/7×7＝11バームにする。これは二等辺三角形の底辺の長さのため直角三角形の底辺は11÷2＝5.5 バームになり、セケドの数値にしたと考えられる。

また、初期形態の腕尺が6バームの定規で円周の長さを計測する場合、腕尺1単位の円周の計算は6バームを使って行う。円周の長さは2π×6バーム＝37.68バームになる。この数値の1/4の9.42バームが1段目の底辺の長さである。この長さの整数倍の段を捜すと10進法の場合と同じく7段目になり9.42×7＝65.94バームになる。この数値を66バームに繰り上げて、腕尺に変換すると66÷6＝11腕尺になる。これは7段目の二等辺三角形の底辺の長さであるので、1段目の長さは11/7腕尺になる。この数値を11にするために腕尺の単位を7バームに変更して11/7腕尺×7バーム＝11バームにする。これは二等辺三角形の底辺の長さのため、直角三角形の長さは11×1/2＝5.5バームになり、セケドの数値にしたと考えられる。

以上の結果をまとめると、腕尺の単位を10単位と6バームに設定して、1段目の二等辺三角形の底辺の長さ求めると、いずれの場合も11/7腕尺になる。その理由は、腕尺の単位の違いに関わらず、底辺と高さの比は「2×3.14×高さ×1/4÷高さ＝1.57」となり一定になるためである。そのため7段目の底辺の長さは1.57×7腕尺＝10.99＝11腕尺となり、1段目の底辺の長さは11/7腕尺になる。この結果を基に、二等辺三角形の底辺の長さを11の整数にするために、腕尺の単位を7バームに変更したと考えられる。なお、腕尺の単位を7バームに変更しても底辺と高さの比は一定のため、底辺の長さは11/7腕尺になり一定である。　　この変更により底辺の長さは11/7腕尺×7バーム＝11バームになり、直角三角形の底辺は11÷2＝5.5 バームになる。この数値をセケドにしたと考えられる。

以上の結果に対して、もし、クフ王のピラミッドの建造の前に、セケドの計算方法が決められていて、1ロイヤルキューピットが7バームに設定されていたとするならば、作図で底辺の長さを求めた時に、腕尺の整数倍となる最小の段数が、偶然に、既定の数値の7に一致したとする考え方は無理と考えられる。以上のことより、クフ王のピラミッドのセケドの算出方法が、ロイヤルキューピットの単位を7バームに設定した根拠となったと考えられる（図-3）。また、二等辺三角形の高さと底辺の長さの計測に、初期形態のロイヤルキューピットの尺度の定規が使われて、その後、その結果に基づいて7バームから成るロイヤルキューピットの定規が作られたと考えられる。その理由は、初期形態のロイヤルキューピットと7バームから成るロイヤルキューピットのバームの長さが同じためである。これについては、次の項目で述べる。