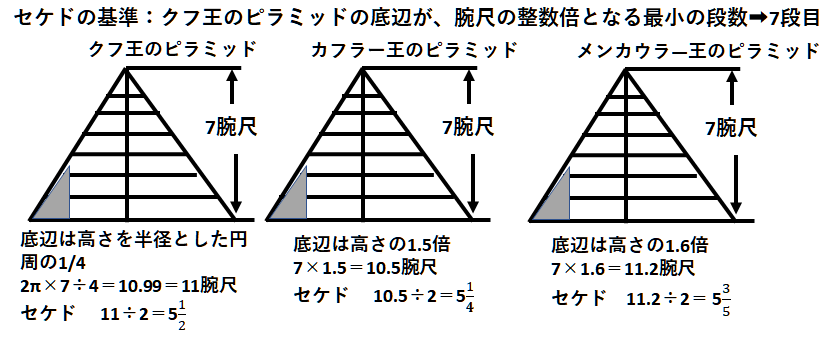
カフラー王、メンカウラー王のピラミッドの　セケドの計算

底辺の長さと高さの比の計算で、クフ王のピラミッドの底辺の長さは、「 高さを半径とした円周の長さの1/4 」、カフラー王とメンカウラー王のピラミッドの底辺の長さは、高さの1.5倍と1.6倍の関係が導き出された。しかし、今までに発表されているセケドの数値、および、測定値を基に計算で求めた 「 底辺の長さと高さの比 」 は、設計当時に設定された正確な数値であるという確証はない。　そのため、これらのセケドを確認し、さらに、底辺の長さと高さの比を確認するために、改めて、計算の方法を、設計当時の底辺と高さの関係に設定して、古代の算術を使ってセケドを計算した。設計当時の底辺の長さは、クフ王のピラミッドでは「高さを半径とした円周の長さの1/4」、カフラー王とメンカウラー王のピラミッドでは、高さの1.5倍と1.6倍　に設定した。

古代の数学について 【 古代のエジプトの数学は、整数の掛け算は、2倍の繰り返しと10倍が使われており、それ以外にはなく、倍増法（2倍法）と呼ばれる計算方法が使われていた。割り算は除数を逆数として掛け算として計算をした。また、分数は単位分数が使われた 】と発表されている（文献-6、ｐ-13、）。さらに、小数点の付いた数値の計算は存在しなかった。古代のエジプトの計算は複雑であるが、古代の計算方法に基づいてセケドを計算した。しかし、分数の計算については、答えを単位分数で表す方法が使われていたが、この計算は複雑であるため、現在の計算方法を併用した（文献-3，ｐ-17～51）。　

セケドについて【 リンドパピルスの幾何学の部のピラミッドに関する問題の中で、傾斜に関する問題が次のように書かれている。（No，56）、「底辺の一辺が360キュービット、高さが250キュービットのピラミッドのセケド（傾斜）を計算する問題　答え5・1/25  掌尺 】（文献-3，ｐ-107～110 、文献-6、ｐ-40 ）。この問題を次のように計算した。最初に、底辺の長さの1ロイヤルキューピットを7バームに換算する。計算は（360×7＝2520）となるが、計算方法は倍増法（2倍法）を使い、A列とB列の数値を設定して、A列とB列の関係から答えを求める。A列の1番目を1として、その次からは、前の数値を2倍にして、1、2、4、８、16、32、64、・・・として列記する。次に、B列の1番目の数値を計算式 （360×7） の360として、次からは前の数値を2倍にして、360、720、1440、2880、・・・・と列記する。その後、A列の中から合計が、計算式（360×7）の 7になる数値を捜す。それは、1番目の1と2番目の2と3番目の4で、合計が1+2+4=7 となる。次に、A列に対するB列の順番の数値を捜す。その数値は1番目の360、2番目の720、3番目の1440で、合計が360+720+1440＝2520となる。その結果、360×7＝360+720+1440＝2520となり、底辺は2520バームとなる。

次に、このピラミッドの高さを1ロイヤルキューピットとした場合の底辺の長さを計算する。計算式は2520÷250となるが、古代のエジプトでは、割り算を掛け算として計算をした。その計算式はX×250＝2520で表される。計算方法は倍増法を使い、A列とB列の数値を設定して、A列とB列の関係から答えを求める。最初に、A列の1番目を1として、その次からは、前の数値を2倍にして、1、2、4、８、16、32、64、・・・と列記する。次に、B列の1番目の数値を計算式（ X×250 ）の250として、その次からは、前の数値を2倍にして250、500、1000、2000、4000・・・・と列記する。次に、B列の中で合計が2520の数値に最も近い数値を捜す。それは、2番目の500と4番目の2000で合計が2500となる。次に、A列からB列の500と2000に対する数値を捜すと2番目の2と4番目の8となる。その数値の合計は2+8=10となる。その結果、2520は500+2000+残り20＝（2+8）×250+20＝10×250+ 20となる。これを、2520÷250の計算式に入れると（10×250+ 20）÷250となる。

しかし、当時の割り算は除数を逆数として掛け算として計算をした。そのため、（10×250+20）÷250＝（10×250+20）×1/250＝10+2/25となる。これは二等辺三角形の底辺の長さのため、直角三角形で表すと（10+2/25 ）÷2＝（ 10+2/25 ）×1/2＝5+1/25となりセケドは5・1/25  となる。

上記の計算を単位分数で行うと次のようになる（文献-8）。初めに、二等辺三角形を直角三角形にして計算をする。底辺の長さは360腕尺×1/2＝180腕尺、高さは250腕尺となる。この数値から「底辺の長さと高さの比」を求めると180÷250＝18/25となる。これを単位分数で表すために分子と分母を18で割ると（18/18）÷（25/18）＝1/1.39となる。1.39は2より小さいため1/1.39は1/2より大きくなる。その結果、底辺の長さと高さの比は180/250＝1/1.39＝1/2+aで表さられる。この関係からaを求めると、180÷250＝18/25＝1/2+aからa=18/25－1/2＝（36－25）/50=11/50となる。11/50は10/50+1/50＝1/5+1/50となるため、底辺の長さと高さの比を単位分数で表すと180/250＝1/1.39＝1/2+a=1/2+1/5+1/50となる。この数値は「直角三角形の底辺と高さの比」のため、セケドを求めるために、これを7倍（バーム）にすると（1/2+1/5+1/50）×7＝（25+10+1）/50×7＝36/50×7＝5.04＝5・1/25となりセケドは5・1/25となる（図-1，）。

カフラー王とメンカウラー王のピラミッドのセケドの計算は倍増法（2倍法）を使い、問題の解答法と同じに行ったが、詳細は省略して要点を示し、現在の数学で行った計算結果を記載した。クフ王のピラミッドの底辺の長さは、円周の長さから求められているため、解答法に準じて計算は出来ない。そのため、幾何学的に算出して5・1/2 の数値を導き出した。　なお、クフ王のピラミッドのセケドの求め方と3基のピラミッドの頂点から最下部までの段数を100段と50段に設定した理由については考察で述べる。

カフラー王のピラミッドのセケドの計算は、頂点から最下部までの高さの段数の100段（100高）を使って行った。高さの1高は3ロイヤルキューピットのため、高さは300ロイヤルキューピットとなる。次に、底辺の長さは高さの1.5倍のため、300×1.5=450となる。 しかし、当時は小数点の付いた数値の計算方法がなかったため、300×1.5＝300×（1+5/10）＝300+300×5×1/10として計算をする。この数式の中の300×5を最初に計算する。倍増法で300×5を求めると1500となる。その数値を300+300×5×1/10の計算式に入れると300∔1500×1/10＝450ロイヤルキューピットとなる。この結果、ピラミッドは高さが300ロイヤルキューピットで、底辺の長さが450ロイヤルキューピットの大きさとなる。この数値を基に前記の問題の解答法に従って、セケドを計算すると5・1/4  となる。これを現在の数学で計算をすると（図-1）、（100高×3腕尺×1.5倍×1/2×7バーム）÷（100高×3腕尺）＝セケド5・1/4  となる（図-1）。

カフラー王のピラミッドのセケドを単位分数で計算をする（文献-8）。二等辺三角形の高さは100段（100高）×3腕尺＝300腕尺、底辺は高さの1.5倍で300×1.5＝450腕尺となる。セケドは直角三角形の底辺の長さで表されるため、底辺の長さ＝450×1/2＝225腕尺、高さは300腕尺で計算をする。底辺と高さの比を求めると、225÷300となるが、この計算を単位分数で行う。そのため、分子と分母を225で割ると（225/225）÷（300/225）＝1/1.333となる。1.333は2より小さいため1/1.333は1/2より大きくなる。 そのため、底辺の長さと高さの比は、225/300＝1/1.333＝1/2+ａで表さられる。 この式からaを求めると　225/300－1/2＝（450－300）/600=150/600＝1/4となる。従って、底辺と高さの比を単位分数で表すと225÷300＝1/1.333＝1/2+a=1/2+1/4となる。この数値を基にセケドを求めるために、7倍（バーム）にすると（1/2+1/4）×7＝5.25＝セケド5 ・1/4となる（図-1）。

メンカウラー王のピラミッドのセケドの計算は、現在の数学を使って頂点から最下部までの高さが50段（50高）、底辺の長さが高さの1.6倍として計算をした。高さは50高×3腕尺＝150腕尺で、底辺の長さは150腕尺×1.6倍＝240腕尺となる。セケドは240×1/2×7÷150＝5.6バーム＝5+3/5となり（図-1）、セケドは5・3/5 となる。

メンカウラー王のピラミッドのセケドを単位分数で計算をする（文献-8）。二等辺三角形の高さは3腕尺×50段（50高）＝150腕尺、底辺は150腕尺×1.6倍＝240腕尺である。セケドは直角三角形の底辺の長さで表されるため、二等辺三角形を直角三角形にして計算をする。そのため、底辺の長さは240÷2＝120腕尺、高さは150腕尺となる。「底辺と高さの比」は120÷150=12/15となる。 この数値を単位分数で表すため、分子と分母を12で割ると（12/12）÷（15/12）＝1/（5/4）＝1/1.25となる。1.25は2より　小さいため1/1.25は1/2より大きくなる。そのため、底辺と高さの比は120/150＝4/5＝1/1.25＝1/2+aで表される。

この式からaを求めるとa＝4/5－1/2=（8－5）/10=3/10=1/10+2/10＝1/10+1/5となる。その結果、「底辺と高さの比」の120/150を単位分数で表すと1/2+a=1/2+1/5+1/10となる。 この数値からセケドを求めるため、7倍（バーム）にすると（1/2+1/5+1/10）×7＝（5+2+1）/10×7＝56/10＝5+6/10となり、セケドは5・3/5 となる（図-1）。

カフラー王とメンカウラー王のピラミッドのセケドを作図で求める方法　　　　　　　　　　　セケドの基準はクフ王のピラミッドの作図を基に設定される。その方法は、高さが7腕尺の二等辺三角形を描き、その1/2の底辺の長さから求められる。そのため、底辺の長さが、カフラー王のピラミッドでは高さの1.5倍、メンカウラ―王のピラミッドでは高さの1.6倍の二等辺三角形を描き、その7段目の辺の長さを腕尺の定規で計り、その1/2の長さからセケドを求める。カフラー王の場合は、7段目の辺の長さは7×1.5＝10.5となり、その1/2の長さは、10.5÷2＝5.25＝5+1/4で、セケドは5・1/4  となる。　メンカウラー王のピラミッドは、7段目の底辺の長さは1.6×7＝11.2となり、その1/2の長さは11.2÷2＝5.6＝5+3/5で、セケドは5・3/5となる。　　　カフラー王とメンカウラー王のピラミッドの「底辺と高さの比」の1.5と1.6は、ピラミッドの測量に基づく計算で確認されたが、設計をした時に、その数値を決めた根拠が明らかでない。これについて考察すると、クフ王のピラミッドの「底辺と高さの比」の1.57を基準にして設定されたと考えられる。クフ王のピラミッドの「底辺と高さの比」は、セケドの作図（図-3）から11腕尺÷7腕尺＝1.57（倍）になる。そのため、この数値の小数点2桁以下を切り捨てた1.5倍をカフラー王のピラミッドの「底辺と高さの比」として、さらに、小数点2桁以下を繰り上げた1.6倍をメンカウラー王のピラミッドの数値に設定したと考えられる。

しかし、小数点の付いた数字の計算は存在しなかったため、単位分数（文献-8）で計算されたと考えられる。クフ王のピラミッドの「底辺と高さの比」の11/7は、（1+4/7）で表すことができるため、この式の4/7の分数を単位分数で計算をする。分子を1にするために、分子と分母を4で割ると4/7＝1/1.75となる。1/1.75は1/2より大きいため1/1.75=1/2+aで表すとことができる。この関係を基にaを求めると、4/7＝1/1.75＝1/2+aからa＝4/7-1/2＝1/14となる。以上のことより、クフ王のピラミッドの「底辺と高さの比」を単位分数で表すと11/7＝1+4/7＝1+1/2+a＝1+1/2+1/14になる。

カフラー王のピラミッドの「底辺と高さの比」は、クフ王のピラミッドの「底辺と高さの比」を基準にして1/14の分数を切り捨てて1+1/2＝1.5倍に設定したと考えられる。メンカウラ―王のピラミッドの「底辺と高さの比」は、クフ王のピラミッドの「底辺と高さの比」を基準にして1/14の分数を1/10に修正して、1+1/2+1/10＝1+6/10＝1.6倍に設定したと考えられる。

次に、底辺と高さの比を基にセケドを計算する。底辺と高さの比は二等辺三角形の1段目の底辺の長さを表しており、底辺の基本単位である。また、セケドは7段目の底辺の長さを基に計算されるため7段目の長さを求める。ｶﾌﾗｰ王のピラミッドの底辺の長さは「1+1/2」腕尺×7段＝「10+1/2」腕尺になる。これは7段目の長さのため1段目の長さは「10+1/2」×1/7になり、さらに、腕尺を7バームにすると「10+1/2」×1/7×7バーム＝「10+1/2」バームになる。これは二等辺三角形の底辺の長さのため直角三角形の底辺の長さは「10+1/2」×1/2＝「5+1/4」バームになり、セケド5・1/4になる。

メンカウラー王のピラミッドのセケドの計算は、底辺と高さの比の「1+1/2+1/10」を使って、前記の計算方法と同じに行った。その計算を簡略化すると、結果は「1+1/2+1/10」腕尺×7段×1/7段×1/2×7バーム＝「5+3/5」バームになり、セケド5・3/5になる。