円の面積を作図で求める方法

5、「 クフ王のピラミッドの底辺の長さは、高さを半径とした円周の長さの1/4 」 とする説を否定した発表について

ピラミッドの測定値とセケドに基づく計算から、「クフ王のピラミッドの底辺の長さは、高さを半径とした円周の1/4」であることが明らかになった。これに対して、この関係を否定した発表がある。しかし、その発表には矛盾があるため、その検証を行った。

クフ王のピラミッドの底辺について、次のように書かれている。【ピラミッドの底辺の周囲は、ピラミッドの高さと同じ長さの半径を持つ円の円周と正確に一致するように造られていたという説は、アーメスの著書とは合致しない。周囲の高さに対する比は、確かに44/7と非常に近く、それは、今日、我々がπの値としてしばしば使う22/7の、ちょうど2倍である。しかし、ここでアーメスのπの値は　約3・1/6で、3・1/7でなかったことを思い出さなければならない。このアーメスのπの値が他のエジプト人たちによっても使われていたことは、12王朝からのパピルスの巻物 （現在、ロンドンにあるカフンパピルス） で立証されている。その中で、円柱の体積を、高さに底面積をかけて求めているが、その底面積はアーメスの方法で決められたものであった。また、パピルスの50問で、書記アーメスは、直径が9の円の面積は1辺が8の正方形の面積に等しいと仮定している。これと現代の式のA=πｒ²と比べると、エジプトのやり方ではπに3・1/6 の値を与えているのに等しく、それは賞賛に値する良い近似値である。さらに、48問において、アーメスは、エジプト人の円面積の式をだすに至った経過を示している。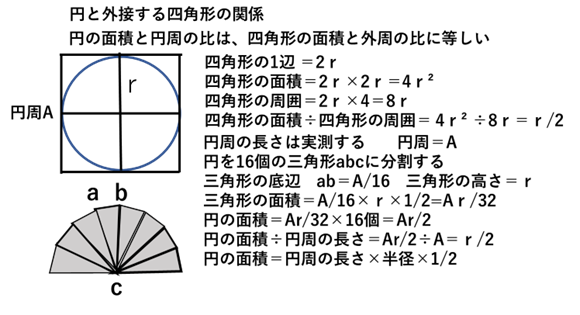それでは、1辺が9の正方形の各辺を3等分して、四隅にできる面積4 の二等辺三角形を切り取り、八角形を作っている。その八角形の面積は63で、1辺が9の正方形に内接する円の面積とそんなに違わず、さらに、1辺が8の四角形の面積とひどくかけ離れてもいない。数値4（8/9）²が本当に我々の定数πに匹敵する役割を演じていたことは、エジプトの円周の求め方から確かめられるようである。それによると、「 円の面積の円周に対にする比は、その円に外接する四角形の面積とその周囲に対する比に等しい 」 となっている。この観察は、比較的良い近似値（4（8/9）²＝3.1605）そのものよりも、正確さは、数学的意味において、はるかにまさる幾何学的関係を明らかにしている。このように、近似値の精度は、とどのつまり数学的、および、建築学的成果を計るよい尺度ではないので、エジプト人の業績のこの面ばかりを強調しすぎることがあってはならない。一方、エジプト人が幾何学図形の相互関係を認識していたということの方は、あまりにもしばしばみ過ごされてきた。また、ナイル川流域で行われた一部の幾何学図形の比較、例えば、円や四角形の周囲と面積の比較は、曲線図形についての歴史上では最初の厳密な言及であった　】　（文献-4、ｐ-23．24、25）。しかし、幾何学図形の厳密な関係の説明はされていない。そのため、円の面積の求め方を検討した。円の面積は、計算で求める方法と作図で求める方法が考えられる。計算で求める方法としては、扇を閉じた状態で二等辺三角形を作り、その面積を計算して、次に、扇を開いた状態にして半円形として、二等辺三角形の面積を合計する。その後、円形の面積を求めたと考えられる。二等辺三角形の面積の求め方は、アーメスの51問で、「 底辺の半分に高さを掛けて求められた 」 と書かれている（文献-4、ｐ-22、　文献-3、ｐ-96）。この方法を検討するため、最初に、円に外接する四角形の面積と周囲の長さを計算した。1辺の長さを円の半径の2倍の2rとして計算すると面積は2ｒ×2ｒ＝4ｒ²、周囲の長さは2ｒ×4＝8ｒとなり、面積と周囲の長さの比は4ｒ²/8ｒ＝r/2となる。次に、円の面積と円周を求めるが、円周の長さを計算で求めることはできない。しかし、その長さは幾何学的に求めることが出来る。それは、円周の長さを実測して、正確な長さを求める方法である。次に、円の面積を求めるが、そのために、円を16個の二等辺三角形に分割して、半円形が8個の二等辺三角形で作られた扇形とする。その後、二等辺三角形の面積を計算するが、底辺の長さを求めるために、円周の長さをAとして、二等辺三角形の底辺の長さをA/16にする。高さを半径の長さのｒとすると、三角形の面積はA/16×ｒ×1/2＝Ar/32となる。円には二等辺三角形が16個あるため、円の面積はAr/32×16＝Ar/2となる。その結果、円の面積÷円周の長さは　Ar/2÷A＝ｒ/2となり、「 外接する四角形の面積と周囲の長さの比」と同じになる。例えば、円周の長さを実測する方法を使って円の面積を計算すると、腕尺が10進法の場合、円周の長さは（図-5）より628/100腕尺になる。この円周の長さを使って円の面積を計算すると（円周の長さ×半径×1/32×16）＝（円周の長さ×腕尺1単位×1/2＝628/100腕尺×1腕尺×1/2＝3.14）になる。現在の計算方法ではπ×1×1＝3.14になり、前記の計算結果と同じになる。

また、初期形態の尺度を使う場合は、腕尺1単位が6バームのため、半径を6バームにして計算をする必要がある。円周の長さは（図-5）より37.68バームのため、円の面積の計算は（円周の長さ×半径×1/32×16）＝（円周の長さ×6バーム×1/2＝37.67×6×1/2＝113.04になる。この数値を腕尺の単位で表す場合、1辺が6バームの面積は6×6＝36であるため、113.04÷36＝3.14になる。

現在の計算では、腕尺1単位が6バームの場合π×6×6＝3.14×6×6＝113.04になり、腕尺の単位で表すと、腕尺1単位の面積が6×6＝36のため、113.04÷36＝3.14になり、前期の結果と同じになる。

しかし、作図の上では、高さと底辺の長さは正確な数値より短くなる。また、この計算式では、円の面積を円周の長さを使って求めているため、この式から円周の長さを求めることは出来ない。

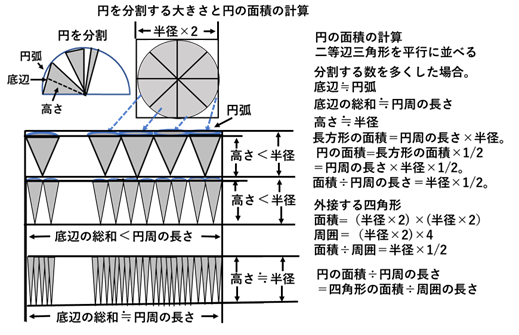
古代の作図による円の面積の求め方

作図でこの関係を明らかにするには、幾何学的に円の面積を導き出して、（ 円の面積÷円周の長さ＝外接する四角形の面積÷外周の長さ ）を証明する必要がある。その方法は、半円形を二等辺三角形で作られた扇形として、その2つの扇形の二等辺三角形を切り離し、さらに、これらの二等辺三角形を横に平行に並べて長方形を作る。次に長方形の横の長さを円周の長さとし、縦の長さを半径の長さとして、長方形の面積を計算する。この方法を使って円の面積を求める。しかし、正確な設定では、二等辺三角形の底辺の総和は円周の長さより短く、高さは半径より短くなる。これを解決するために、円を分割する数を多くして、切り離した二等辺三角形の底辺を円弧の長さに近づけて、その総和を円周の長さに近づける。さらに、この方法により、高さを半径の長さに近づける。これにより、長方形の「横の長さ≒円周の長さ」となり、「縦の長さ≒半径の長さ」となる。その結果、長方形の面責は「円周の長さ×半径の長さ」となる。長方形を作る二等辺三角形の数は、円から作られる数の2倍となるため、円の面積は長方形の面積の1/2となる。そのため、円の面積÷円周の長さは、「円周の長さ×半径×1/2÷円周の長さ＝半径×1/2 」 となる。次に、外接する四角形の面責を計算すると（半径×2）×（半径×2）となり、外周は（半径×2）×4となる。この面積と外周の比は（半径×2）×（半径×2）÷（半径×2×4）＝半径×1/2となる。この結果、円と外接する四角形の幾何学図形の関係が明らかになった（図-6）。さらに、現在の数学を使って「円の面積と円周の長さの比」を計算すると、πｒ²÷　2πｒ＝ｒ/2になり、前記の結果と同じになる。このことは、円周率とπr²、2πｒの計算の概念がなくても、円とそれに外接する四角形との正確な幾何学的関係を認識していたと考えられる。これにより、「曲線図形についての厳密な言及」は証明された。

例えば、円周の長さを実測する方法を使って円の面積を計算すると、腕尺が10進法の場合の円周の長さは（図-5）より628/100腕尺になるため、「円周の長さ×半径×1/2」は（628/100×1×1/2＝3.14）になる。現在の計算方法ではπ×1×1＝3.14になり、前記の計算結果と同じになる。

また、初期形態の尺度を使う場合は、腕尺1単位が6バームのため、半径を6バームにして計算をする必要がある。円周の長さは（図-5）より37.68バームのため、円の面積の計算は「円周の長さ×半径×1/2」＝（37.68×6×1/2＝113.04）になる。この数値を腕尺の単位で表すには、腕尺1単位の面積が6×6＝36のため、113.04÷36＝3.14になる。現在の計算では、腕尺1単位が6バームの場合π×6×6＝3.14×6×6＝113.04になり、腕尺の単位で表すと、腕尺1単位の面積が6×6＝36のため、113.04÷36＝3.14になり、前期の結果と同じになる。　しかし、前記の2つの方法は、円の面積を円周の長さを使って求めているため、この方法から円周の長さを求めることは出来ない。その解決策として、円周を実測して長さを求めることが、正確な円周の長さの算出方法となる。