作図による円の面積の計算

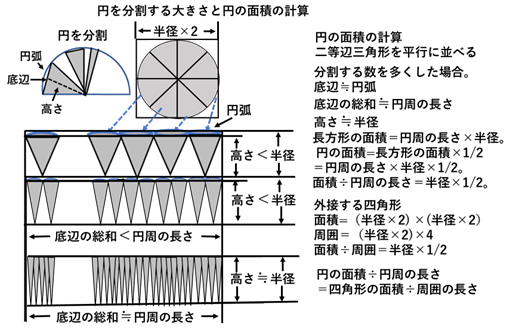
「円の面積の円周に対にする比は、その円に外接する四角形の面積とその周囲に対する比に等しい 」という関係を作図で明らかにするには、幾何学的に円の面積を導き出して、（ 円の面積÷円周の長さ＝外接する四角形の面積÷外周の長さ ）を証明する必要がある。その方法は、半円形を二等辺三角形で作られた扇形として、その2つの扇形の二等辺三角形を切り離し、さらに、これらの二等辺三角形を横に平行に並べて長方形を作る。次に長方形の横の長さを円周の長さとし、縦の長さを半径の長さとして、長方形の面積を計算する。この方法を使って円の面積を求める。しかし、正確な設定では、二等辺三角形の底辺の総和は円周の長さより短く、高さは半径より短くなる。これを解決するために、円を分割する数を多くして、切り離した二等辺三角形の底辺を円弧の長さに近づけて、その総和を円周の長さに近づける。さらに、この方法により、高さを半径の長さに近づける。これにより、長方形の「横の長さ≒円周の長さ」となり、「縦の長さ≒半径の長さ」となる。その結果、長方形の面責は「円周の長さ×半径の長さ」となる。長方形を作る二等辺三角形の数は、円から作られる数の2倍となるため、円の面積は長方形の面積の1/2となる。そのため、円の面積÷円周の長さは、「円周の長さ×半径×1/2÷円周の長さ＝半径×1/2 」 となる。次に、外接する四角形の面責を計算すると（半径×2）×（半径×2）となり、外周は（半径×2）×4となる。この面積と外周の比は（半径×2）×（半径×2）÷（半径×2×4）＝半径×1/2となる。この結果、円と外接する四角形の幾何学図形の関係が明らかになった（図-6）。さらに、現在の数学を使って「円の面積と円周の長さの比」を計算すると、πｒ²÷　2πｒ＝ｒ/2となり、前記の結果と同じになる。このことは、円周率とπr²、2πｒの計算の概念がなくても、円とそれに外接する四角形との正確な幾何学的関係を認識していたと考えられる。これにより、「曲線図形についての厳密な言及」は証明された。

例えば、円周の長さを実測する方法を使って円の面積を計算すると、腕尺が10進法の場合の円周の長さは（図-5）より628/100腕尺になるため、「円周の長さ×半径×1/2」は（628/100×1×1/2＝3.14）になる。現在の計算方法ではπ×1×1＝3.14になり、前記の計算結果と同じになる。また、初期形態の尺度を使う場合は、腕尺1単位が6バームのため、半径を6バームにして計算をする必要がある。円周の長さは（図-5）より37.68バームのため、円の面積の計算は「円周の長さ×半径×1/2」＝（37.68×6×1/2＝113.04）になる。この数値を腕尺の単位で表すには、腕尺1単位の面積が6×6＝36のため、113.04÷36＝3.14になる。現在の計算では、腕尺1単位が6バームの場合π×6×6＝3.14×6×6＝113.04になり、腕尺の単位で表すと、腕尺1単位の面積が6×6＝36のため、113.04÷36＝3.14になり、前期の結果と同じになる。しかし、この方法は、円の面積を円周の長さを使って求めているため、この方法から円周の長さを求めることは出来ない。その解決策として、円周を実測して長さを求めることが、正確な円周の長さの算出方法となる。

Follow me!