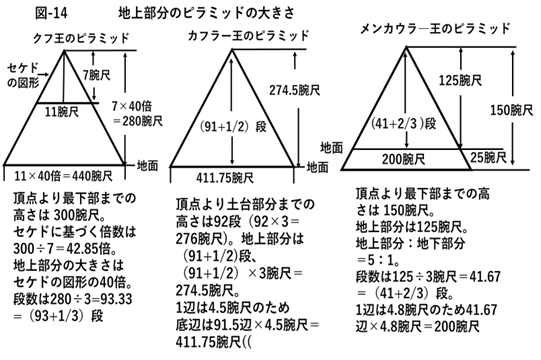
地上部分の大きさ
tugumasab32地上部分のピラミッドの高さと底辺の長さ
高さは頂点より最下部までの段数で決められるが、ピラミッドが岩盤の上に建造されている場合、地下部分の建造が行われないため、高さと底辺の長さの決定方法について検討した。クフ王のピラミッドは高さが280腕尺、底辺の長さが440腕尺に設定されている（表-2）。しかし、その理由が明らかでない。ピラミッドの角度はセケドに基づいて設定されている。その基準は、クフ王のピラミッドのセケドを、作図により計算する方法から求められている。それは直角三角形の高さを7段（7腕尺）とした場合の底辺の長さから計算される（図-3）。そのため、高さの腕尺7単位を基準値にして、その倍数を計算した。頂点から最下部までは100段×3腕尺=300腕尺のため、300腕尺÷7腕尺＝42.86倍となる。
この中の40倍の部分を設計、測量、建造の行い易い高さとして、7腕尺×40＝280腕尺を地上部分に設定したと考えられる。また、セケドを表す二等辺三角形の底辺の長さは11腕尺となるので（図-3）、その40倍の440腕尺を底辺の長さにしたと推測した。しかし、段数を基に高さと底辺の長さを検討すると、段数は1段が3腕尺のため、280÷3=(93+1/3)=93.33段となり端数の付いた数値となる。その解決策として、地面より2/3段低い94段目を地上部分の建造の起点として、完成後に掘り下げた所を埋めて、地上の起始部を(93+1/3)段に戻したと考えられる。また、底辺の長さは94段目より「1辺×段数」で設定されるため、93.33段の底辺は93.33辺となり、腕尺で表すと1辺が4.713腕尺のため93.33×4.713＝439.86＝440腕尺となる。大きなピラミッドの建築方法はクフ王のピラミッドで完成されたと考えられる。クフ王とカフラー王のピラミッドの頂点から最下部までの高さは300腕尺で同じであるが、地上部分の高さはクフ王のピラミッドは280腕尺、カフラー王のピラミッドは274.5腕尺（表-2）で、5.5腕尺の差がある。しかし、その数値は小さいため有意義な差ではないと考えられる。このことを考察すると、初めは、カフラー王のピラミッドは、クフ王のピラミッドの高さと同じに設計されたと推測される。しかし、カフラー王のピラミッドの建築地盤がクフ王の地盤より高いため、クフ王のピラミッドの高さに合わせるために、高さを274.5腕尺に修正したと考えられる。これに基づいて段数を計算すると、段数は274.5÷3＝91.5＝（91+1/2）段となり、構築し易い数値となる。しかし、ピラミッドと地面の接続部分を整えるために深さが必要となるため、1/2段下の92段目をピラミッド建造の起始部として、完成後に掘り下げた1/2段の部分を埋めて、(91+1/2)段の高さに戻したと考えられる。底辺の長さは1辺が4.5腕尺のため、91.5段目は91.5×4.5＝411.75腕尺となり（表-2）の結果の411.84腕尺と同じになる。
メンカウラー王のピラミッドの高さは125腕尺（表-2）である。頂点から最下部までの高さは150腕尺のため、地下部分の深さ を25腕尺にして、地上部分と地下部分の高さの比を(5：1)に設定したと考えられる。この比の決め方は、地上部分と地下部分を（1：1），（2：1），（3：1），（4：1），（5；1）として計算をして、その結果、（5：1）の場合の高さの数値が150腕尺×5/6＝125腕尺となるので、これを地上部分の大きさに設定したと推測される。段数は125÷3＝（41+2/3）＝41.67段となる。そのため、地面より1/3段低い42段目を地上部分の起始部としてピラミッドを建造して、完成後に掘り下げた1/3段の部分を埋めて、地上部分の高さを（41+2/3）＝41.67段に戻したと考えられる。底辺の長さは1辺が4.8腕尺のため、41.67段目は41.67×4.8＝200腕尺となり、（表-2）の結果の200.016腕尺と同じ長さになる。
なお、ピラミッドの建造には、起始部の段を水平に造ることが重要である。そのためには、地下部分の底面の位置を正確に設定する必要がある。それを設計で行う場合、1段は腕尺3単位のため、1/3段と2/3段は腕尺の1単位と2単位になるので、深さを設定する際に都合が良い深さの数値であると考えられる。
Follow me!
